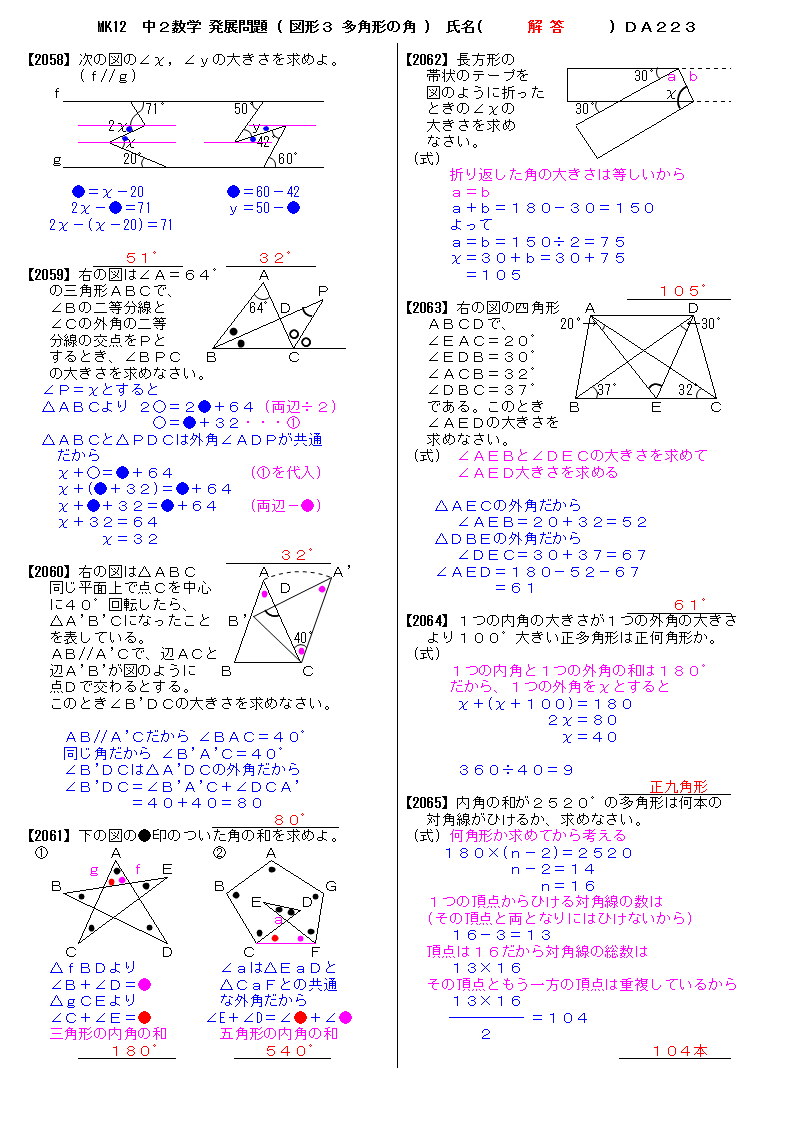
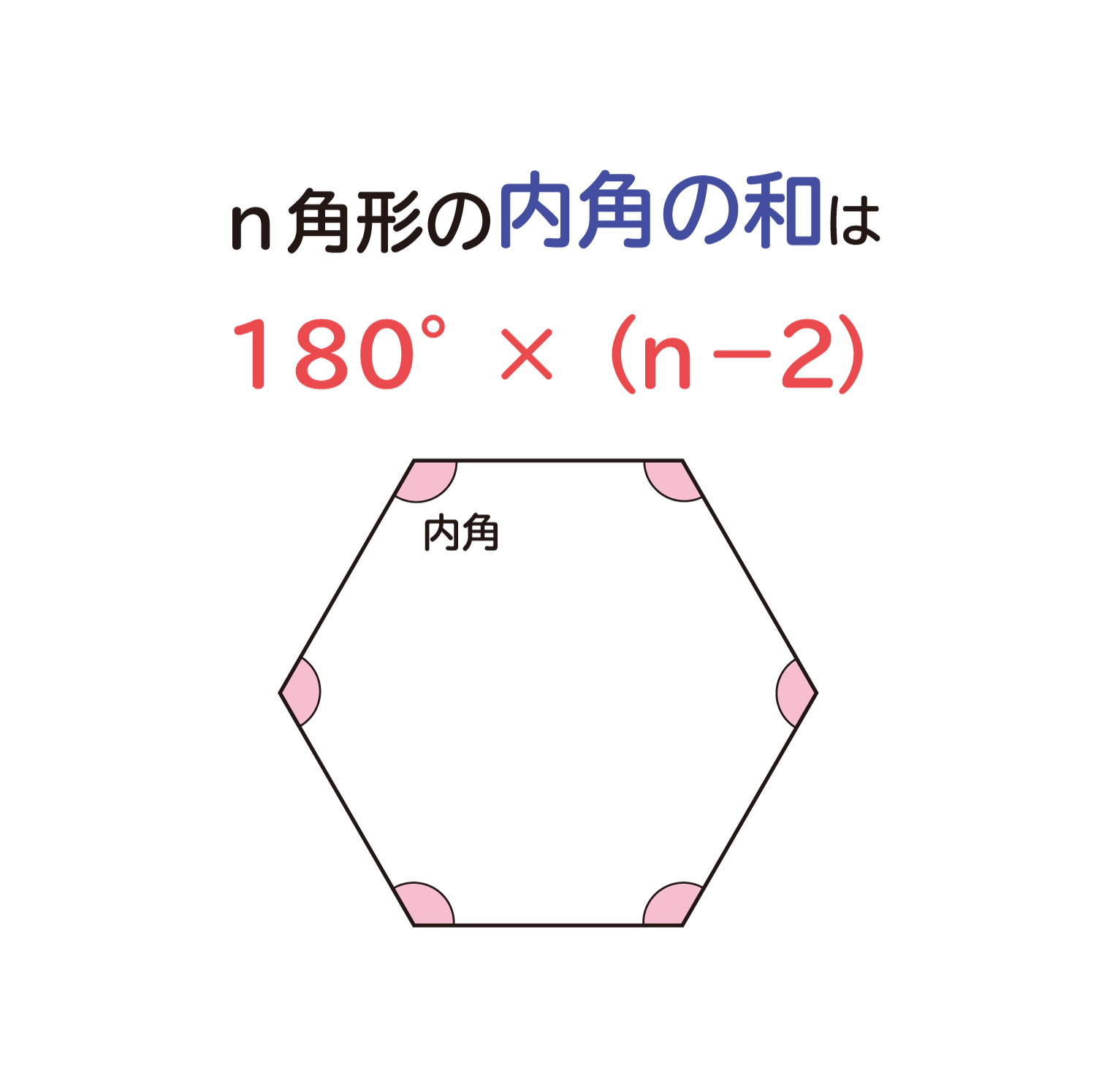
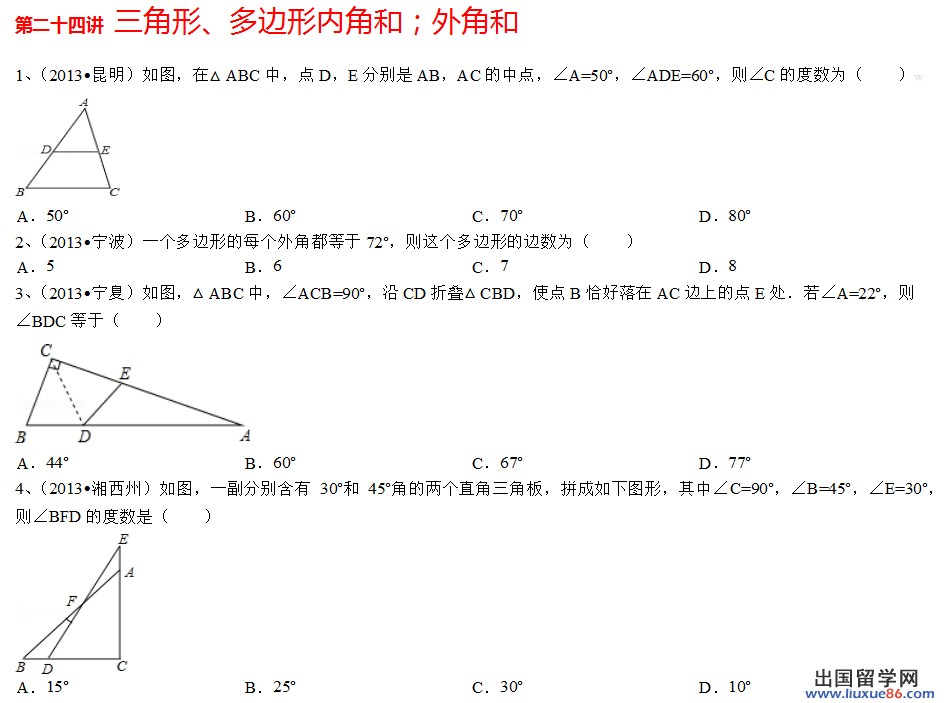
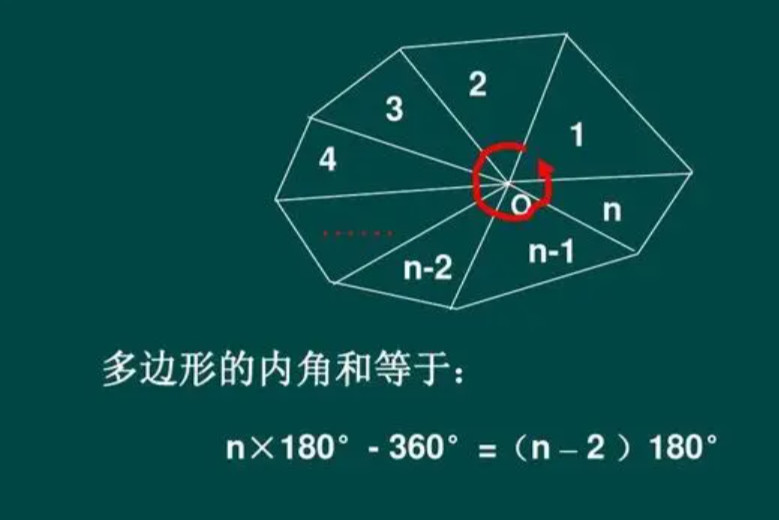
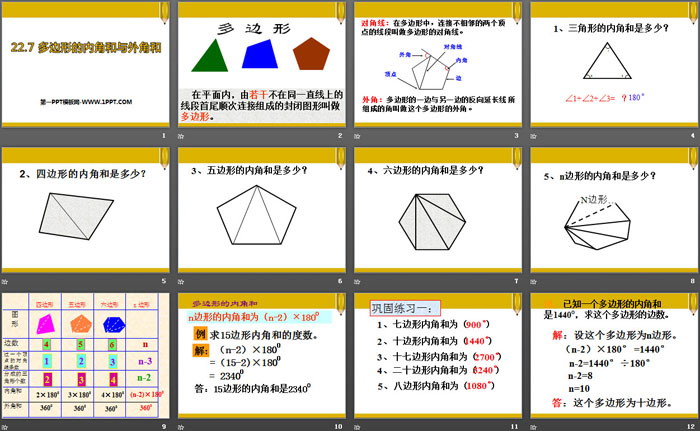
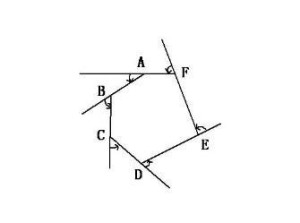
多边形的内角和与外角和 我们早已接触过,三角形的内角和为180度,四边形的内角和为360度,但是好像严格证明过的很少。 我们现在已是初二,该严谨证明他们啦。 三角形和四边形的
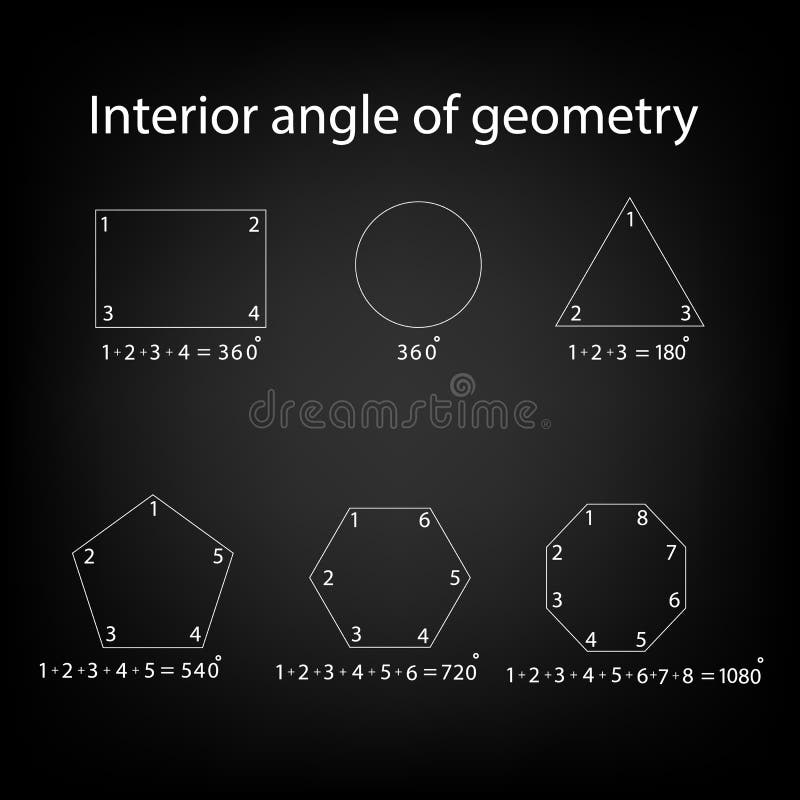
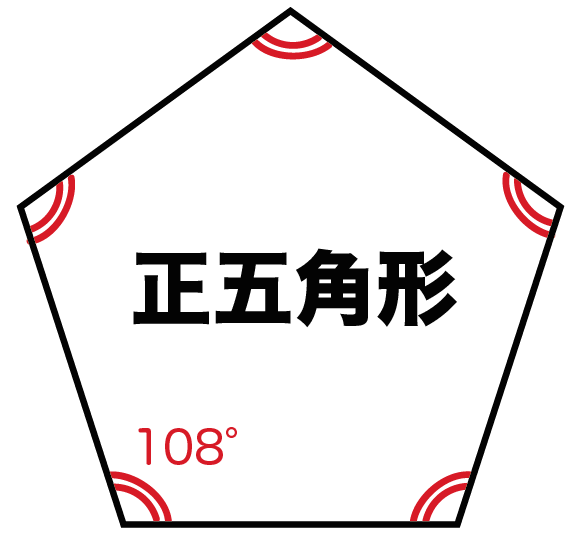
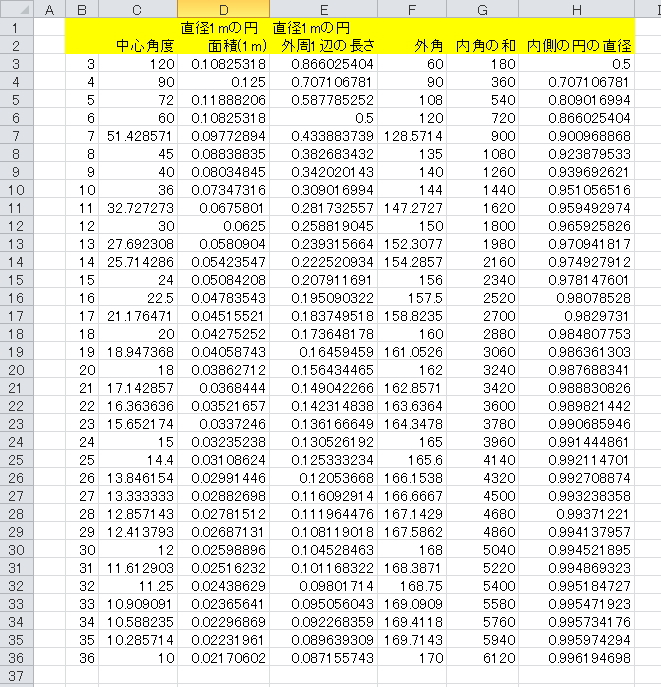
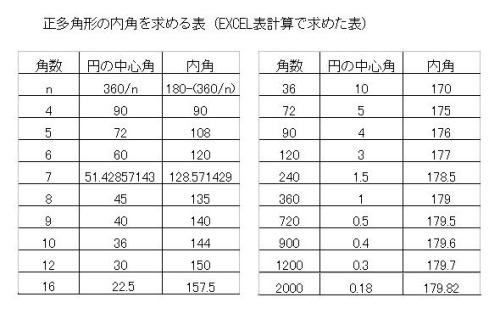
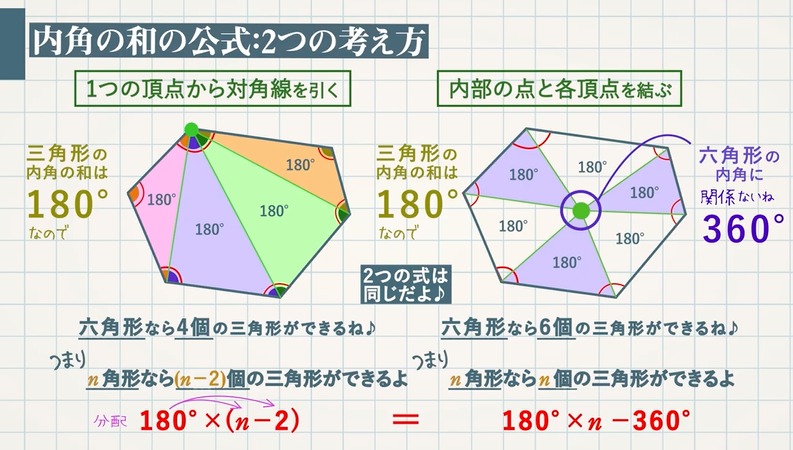
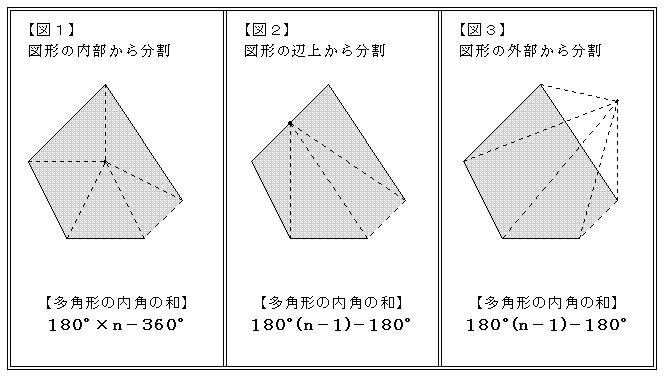
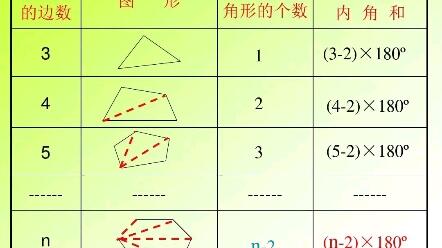
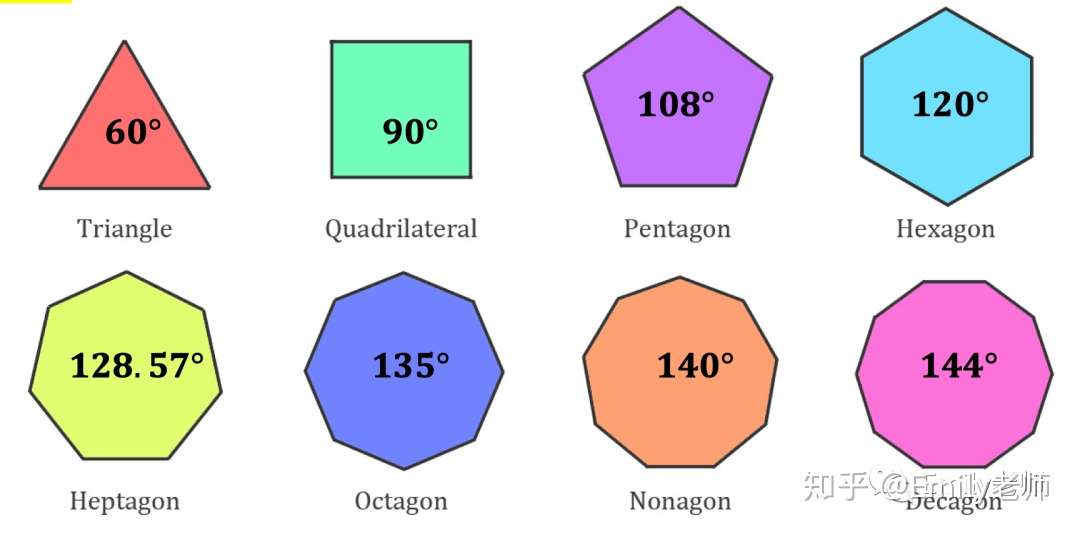
多角形 内角 一覧-正九角形の1つ分の内角は\(=140°\) 正十角形の1つ分の内角は\(=144°\) 正十二角形の1つ分の内角は\(=150°\) と求めてやることができます。 内角の和を考える方法 次は内角の和三角形の内角の和が180°なのでn角形の内角の和は 証明B 多角形の内部に一つの点をとりそこから各頂点に線分を引くと多角形の内部にn個の三角形ができる。 この三角形の内角のうち内部に取った
多角形 内角 一覧のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「多角形 内角 一覧」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
 |  | |
「多角形 内角 一覧」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
 | ||
「多角形 内角 一覧」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 | ||
 |  |  |
 |  |  |
「多角形 内角 一覧」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
 |  |  |
「多角形 内角 一覧」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 | ||
 |  | |
 | ||
「多角形 内角 一覧」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 | ||
「多角形 内角 一覧」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
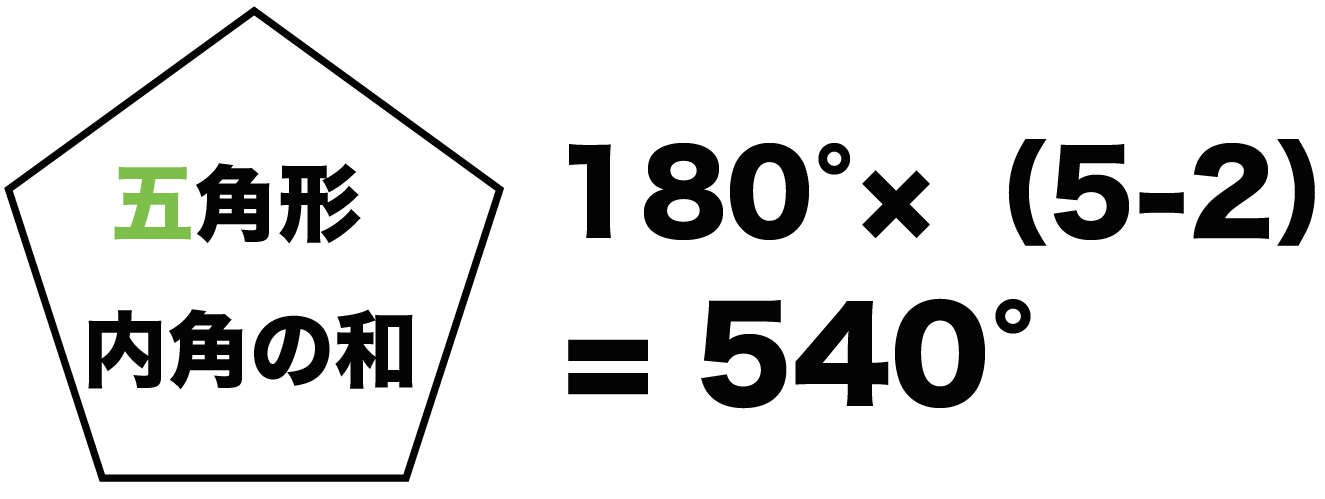 |  | |
 |  |  |
「多角形 内角 一覧」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 | 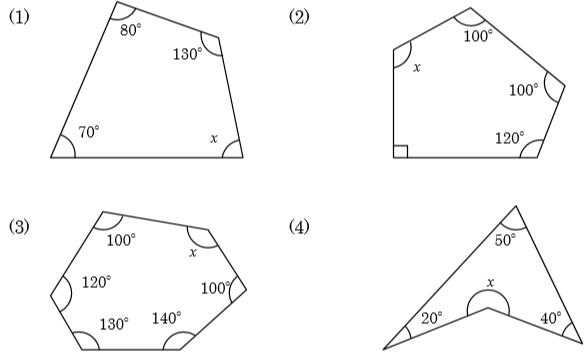 |
正多角形(せいたかっけい、せいたかくけい、regular polygon)とは、全ての辺の長さが等しく、全ての内角の大きさが等しい多角形である。 なお、この記事では n は を満たす数とする。 正多角 2 回答 中学校ではなぜ凹n角形の内角の和が (n2)×180°であることを使ってはいけないのでしょうか? 凸n角形であっても凹n角形であっても、内角の和が (n2)×180°となるのは全く
Incoming Term: 多角形内角和, 多角形 内角, 多角形 内角 公式, 多角形 内角の和, 多角形 内角の和 小学生, 多角形 内角 プリント, 多角形 内角 一覧, 多角形 内角の和 プリント, 多角形 内角の和の求め方, 多角形 内角を求める公式,




0 件のコメント:
コメントを投稿